Logarithmes

Wikipédia : [1]

Les fonctions logarithmiques sont les réciproques des fonctions exponentielles car elles sont bijectives (C'est-à-dire que tout élément de l'ensemble d'arrivée a un et un seul antécédent [2] ).

Si 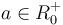$a \in R_0^+$ alors le logarithme en base a d'un réel strictement positif est l'exposant de la puissance de a égale à ce réel.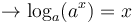$\rightarrow \log_a (a^x) = x$

Quelques propriétés et définitions à retenir :

• $log_a (y) = x \Leftrightarrow y = a^{x}$
• $log_{10} \left ( x \right ) = log (x)$
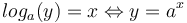
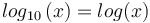
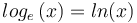• $log_{e} \left ( x \right ) = ln (x)$ (logarithme népérien)
• $log_a \left ( u.v \right ) = log_a u + log_a v$
• $log_a \left ( \frac{u}{v} \right ) = log_a u - log_a v$
• $log_a \left ( u^n \right ) = n.log_a (u)$

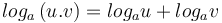
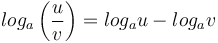
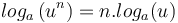
Attention ! Ne pas oublier le domaine de définition !!

Conditions d'existences : 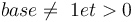$base \ne \ 1 et > 0$

Le logarithme népérien: [3]