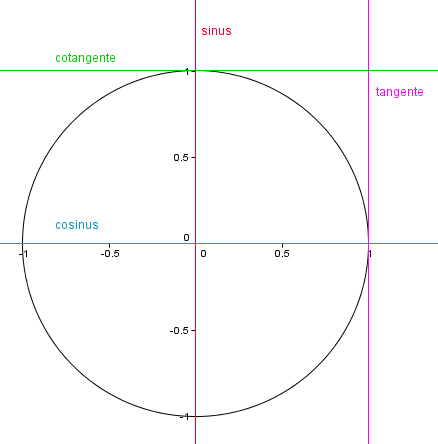
Formules de base
 : vient de pythagore, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés
: vient de pythagore, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés

Formules d'addition






Formules de duplication



Formules de Carnot


Formules de Simpson
 : vient de pythagore, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés
: vient de pythagore, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés











