Maths

Voici une version "simplifié", qui correspond à ce qui doit être maîtrisé pour s'en sortir en math dans le secondaire...

Arithmétique

Ensembles mathématiques

• Naturels(Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \mathbb{N}} ): 0, 1, 2, 3, 4, 5, 6, 7...
• Entiers(Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \mathbb{Z}} ): 0, 1, -15, 7, -8 752 366...
• Décimaux(Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \mathbb{D}} ): 5.0, 2.3, 0.089...
• Rationnels(Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \mathbb{Q}} ): 0.33333, 6/17...
• Réels(Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \mathbb{R}} ): Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \sqrt{2} } , Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \pi } , ... (Ces deux exemples peuvent aussi être appelés "nombres irrationnels")
• Complexes(Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \mathbb{C}} ): 5+8i, 7+i... (en 6ème)

NB : Un nombre irrationnel est un nombre réel qui n'est pas rationnel, c'est-à-dire qu'il ne peut pas s'écrire sous la forme d'une fraction Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \frac{a}{b}} , où a et b sont deux entiers relatifs (avec b non nul).

NB : Un nombre naturel est un nombre entier qui est un nombre décimal qui est un rationnel qui est un réel et qui est un complexe. Mais un complexe n'est pas forcément un réel, ni rationnel, ni décimal, ni entier, ni naturel.

Erreur lors de la création de la vignette : Fichier manquant

Priorité des opérations

• Ordre à suivre:
  • Parenthèses
  • Puissances
  • Multiplications/divisions
  • Additions/soustractions

        Théorie et exemples Partie 1

        Théorie et exemples Partie 2

     -> Exercices

Fractions

• additions/soustractions simplifiées (addition soustraction de fractions expliqués)
  • Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \frac{2} {3} - \frac{4}{5} = \frac{2*5}{3*5} - \frac{4*3}{5*3} =\frac{10}{15}- \frac{12}{15} = \frac{10 - 12}{15} = \frac{-2}{15} }
• multiplications/divisions

Algèbre

Les règles de l'arithmétique s'appliquent [exemple de CE]

conditions d'existence

• fractions : le dénominateur doit être différent de zéro

ex : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \frac{1}{x} \Rightarrow \; x \ne \; 0} ou Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \frac{4+x}{2-x} \Rightarrow \; 2-x \ne \; 0 \Rightarrow \; -x \ne \; -2 \Rightarrow \; x \ne \; 2}

• racines d'un nombre pair : ce qui est compris sous la racine doit être Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle >0}
• tangentes/cotangentes
• fonctions réciproques (arcsin,arctan,..)
• logarithmes

produits remarquables

1. Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle (A+B)^2= A^2+2*A*B+B^2}
2. Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle (A-B)^2= A^2-2*A*B+B^2}
3. Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle (A+B)*(A-B)= A^2-B^2}
4. produits remarquables

Analyse

[études de fonctions]

[1]

• notations
• domaine
• racines : on égale la fonction à zéro puis isole x. Ex : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle 5+3x=0 \Rightarrow \; x= \frac{-5}{3}}
• asymptotes
• intersection avec l'axe OY : on remplace x par 0. Ex : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle f(x)= 5+3*x+x-1 \rightarrow f(0)= 5+0+0-1 = 4}
• parité
  • si f(x) = f(-x) alors la fonction est paire
  • si f(-x) = -f(x) alors la fonction est impaire
• tableaux (signe, croissance, concavité)
  • on place les racines de la dérivée première et la dérivée seconde ainsi que leurs signe
    • dérivée première : Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle >0 \Rightarrow fonction \nearrow \; ; <0 \Rightarrow fonction \searrow \; }
    • si dérivée seconde positive alors fonction avec concavité Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \cup } si dérivée seconde négative alors fonction avec concavité Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle \cap }
• représentations (graphique)

Types

• droites
• paraboles
• homographiques
• exponentielles
• logarithmes

Trigonométrie

dans les triangles

• formules de base

dans le cercle

• valeurs

• sinus

• cosinus

• tangente

formules

Formules trigo dans le cercle

Formule fondamentales	Formules de base	Formules d'addition	Formules de duplication	Formules de Carnot	Formules de Simpson
Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle cos^2(x) + sin^2(x)= 1 }	Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle tan(x)= \frac{sin(x)} {cos(x)} }	Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle cos(a+b)= cos(a)cos(b)-sin(a)sin(b) }	Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle sin(2a)= 2sin(a)cos(a) }	Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle 1+cos(2a)= 2cos^2(a) }	Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle sin(p)+sin(q)= 2sin \left ( \frac{p+q} {2}\right ) cos \left ( \frac{p-q} {2}\right ) }
		Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle cos(a-b)= cos(a)cos(b)+sin(a)sin(b) }	Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle cos(2a)= cos^2(a)-sin^2(a) }	Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle 1-cos(2a)= 2sin^2(a) }	Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle sin(p)-sin(q)= 2sin \left ( \frac{p-q} {2}\right ) cos \left ( \frac{p+q} {2}\right ) }
		Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle sin(a+b)= sin(a)cos(b)+sin(b)cos(a) }			Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle cos(p)+cos(q)= 2cos \left ( \frac{p+q} {2} \right ) cos \left ( \frac{p-q} {2}\right ) }
		Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle sin(a-b)= sin(a)cos(b)-sin(b)cos(a) }			Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle cos(p)-cos(q)= -2sin \left ( \frac{p+q} {2}\right ) sin \left ( \frac{p-q} {2}\right ) }
		Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle tan(a-b) = \left ( \frac{tan(a) - tan(b)} {1 + tan(a)tan(b)}\right ) }
		Échec de l’analyse (SVG (MathML peut être activé via une extension du navigateur) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://wikimedia.org/api/rest_v1/ » :): {\displaystyle tan(a+b) = \left ( \frac{tan(a) + tan(b)} {1 - tan(a)tan(b)}\right ) }

calcul intégral

définition

• définition: une fonction F(x), dont la dérivée est f(x), s'appelle primitive de f(x).

• • exemple:

la primitive de f(x)=3x² est est F(x)=x³ ou F(x)=x³+1 ou encore F(x)=x³-1 ==> F(x)=x³+k où k est une constante et la dérivéé d'une constante vaut toujours 0 donc la primitive de f(x)=3x² a une infinité de réponses (F(x)=x³+k).

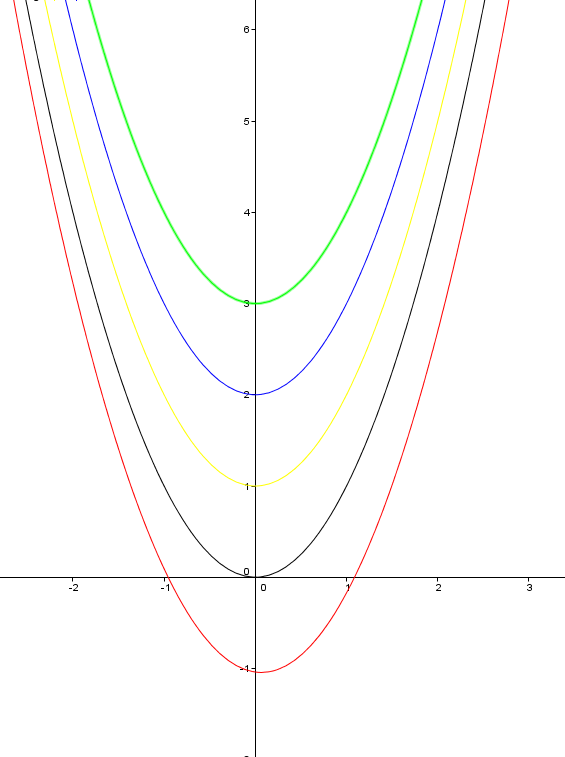
• • preuve:

la fonction noire: f(x)=x²

           verte: f(x)=x²+3
           jaune: f(x)=x²+1
           rouge: f(x)=x²-1
           bleue: f(x)=x²+2

si on dérive chaque fonction on obtient f'(x)=2x. On a prouvé que les dérivées sont les mêmes pour toutes les fonctions et elles varient des unes des autres à une constante près . ==> la dérivé d'une constante "k"=0

• La dérivée première ne change pas, sauf les extrémum changent en ordonnées, l'axe Oy.

 car (x²)'=2x
 car (x²+1)'=2x

• La dérivée seconde ne change pas non plus car les concavités restent les mêmes.

 car (2x)'=2
 car (2x)'=2

MAIS une primitive f(x)=3x² qui s'annule en x=3 ne peut être F(x)=x³-3. Il n'y a qu'un endroit où cette fonction s'annule en x=3.